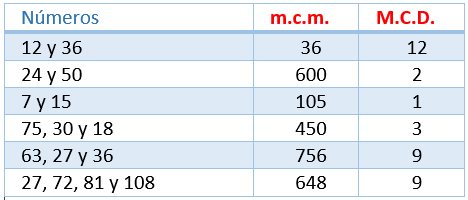
Cálculo del mínimo común múltiplo (m.c.m.)
El mínimo común múltiplo (m.c.m.) de dos o más números a, b, c, d… es el menor de los múltiplos comunes a dichos números. Se representa por:
m.c.m. (a, b, c, d…)
Ejemplo.
Halla el mínimo común múltiplo de 4 y 6.
M(4) = {4, 8, 12, 16, 20, 24, 28, 32, 36...}
M(6) = {6, 12, 18, 24, 30, 36, 42...}
Los múltiplos comunes de 4 y 6 son: {12, 24, 36...}
De todos ellos, el menor es el número 12.
Se escribe: m.c.m. (4, 6) = 12
En la práctica y para números grandes, el cálculo del m.c.m. de dos o más números se realiza por descomposición factorial.
1º Se realiza la descomposición factorial de los números dados.
2º Se seleccionan y se multiplican los factores primos comunes y no comunes elevados al mayor exponente.
Ejemplo.
Halla el mínimo común múltiplo (m.c.m.) de 45 y 60.
.jpg)
.jpg)