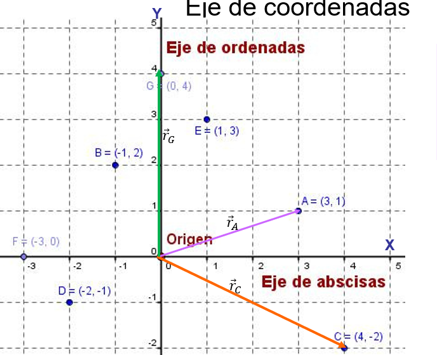
El vector de posición, \(\vec{r}\) es el vector que une el origen con el lugar que ocupa el cuerpo en un instante determinado. Tendrá un módulo (valor), una dirección y un sentido (punta de la flecha). Este vector vendrá definido por unas coordenadas cartesianas (x, y), si estamos en el plano (dos dimensiones) o (x, y, z, ) si estamos en el espacio (tres dimensiones). Si hacemos coincidir el punto inicial del vector con el origen de coordenadas O (0,0), el vector vendrá dado por las coordenadas del extremo final (punta de la flecha). 

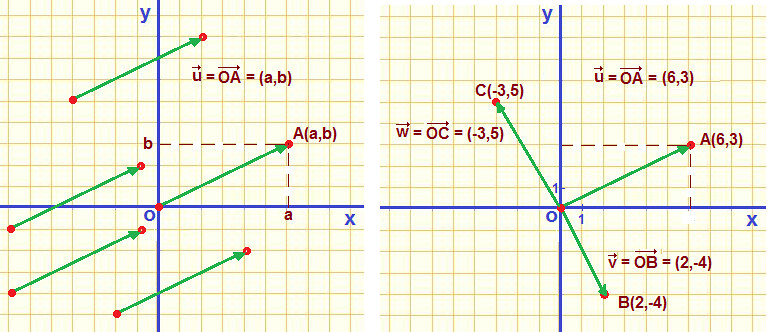
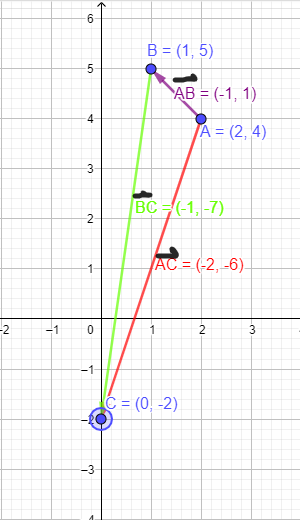
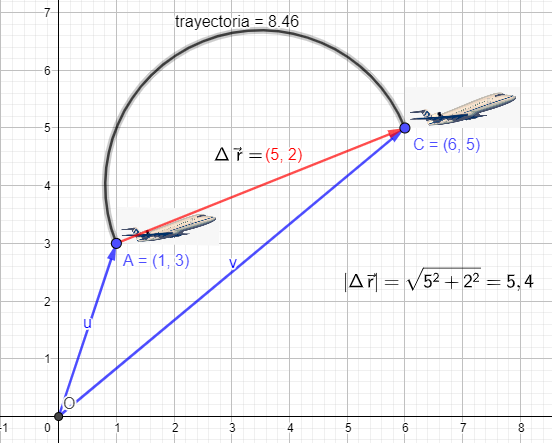
En el caso que el punto inicial no coincidiese con el origen de coordenadas, las componentes del vector de extremos  A (x₁ , y₁ ) y B (x₂ ,y₂ ),  podemos obtenerlas restando a las coordenadas del punto B (punto de la flecha) las del A (punto inicial). \[\boxed{\vec{AB}=(x_2-x_1,y_2-y_1)}\]

En el caso que estuviésemos en el espacio (tres dimensiones) el procedimiento es similar A (x₁ , y₁ , z₁ ) , B (x₂ ,y₂, z₂ ) \[\boxed{\vec{AB}=(x_2-x_1,y_2-y_1,z_2-z_1)}\]

A parte de poder representar un vector con sus coordenadas también podemos representarlo utilizando la ecuación vectorial asociada a las coordenadas de nuestro vector.

La ecuación vectorial, en el plano, asociada a un vector de coordenadas (a,b) viene dada por : \[\boxed{\vec{r}=a\vec{i}+b\vec{j}}\]

Los vectores, \(\vec{i}\) y \(\vec{j}\), son vectores unitarios asociados a los ejes x e y respectivamente, el \(\vec{i}\) tendría como coordenadas el (1,0) y el \(\vec{j}\) sus coordenadas serían (0,1).

Módulo de un vector: es la longitud de un segmento orientado en un espacio que está determinado por dos puntos y el orden de estos. En otras palabras, el módulo de un vector es la longitud entre el inicio y el final del vector, es decir, dónde empieza y dónde termina la flecha. Se representa como |\(\vec{u}\)|

Para calcular el módulo de un vector \(\vec{u}\) de coordenadas (x,y) utilizaremos la siguiente expresión: \[\boxed{|\vec{u}|=\sqrt{x^2+y^2}}\]

El desplazamiento, es una magnitud vectorial que nos indica el cambio de posición que experimenta un cuerpo en movimiento. Para trazar el vector desplazamiento,\(\Delta\vec{r}\), siempre trazaremos la línea recta (vector) que une el punto inicial (punto de partida) con el punto final (punto de llegada) y para calcularlo, recuerda, que al punto final le restamos el punto inicial. Por tanto, sólo coincidiría con la trayectoria si esta última fuese una línea recta. Teniendo en cuenta que la distancia recorrida o espacio recorrido se mide sobre la trayectoria tampoco coincidirá con el desplazamiento, excepto si fuese rectilínea la trayectoria y no cambiase de sentido de movimiento. Es importante razonar que si el punto inicial y final coinciden el desplazamiento sería nulo.

No hemos especificado en el dibujo las unidades al no estar definidas en los ejes, si el problema nos habla de kilómetros, expresamos nuestro resultado final en Km. Para calcular la distancia sobre la trayectoria vemos que el avión ha recorrido la mitad de la longitud de la circunferencia trazada (es una semicircunferencia). Recordar que la longitud de una circunferencia viene dado por L=2πR, el radio vendrá dado por la mitad del diámetro (módulo del vector desplazamiento).