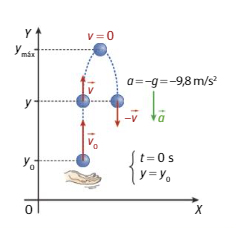
Observa la siguiente imagen y resuelve los apartados indicados:
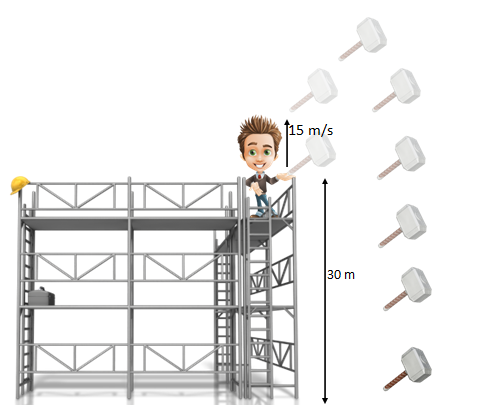
- ¿Qué altura máxima alcanza el martillo al lanzarlo?
- ¿Qué tiempo tarda el martillo en llegar al punto más alto?
- ¿Cuánto tiempo pasó desde el lanzamiento hasta que se encuentra a la mitad de altura del andamio?
- ¿Qué velocidad llevaba el martillo en el punto anterior?
- ¿Qué tiempo tardó en llegar al suelo desde el momento del lanzamiento?
- ¿Con qué velocidad llegó al suelo el martillo?
En primer lugar identificamos los datos que nos dan, Vo=15 m/s y altura del andamio, será la posición inicial, yo=30 m respecto del suelo. Para resolver los distintos apartados planteamos en primer lugar las ecuaciones de movimiento de nuestro cuerpo, la de posición y la de velocidad: la ecuación de posición vendrá dada por: \[ y_f = y_0 + V_o.t - \frac{g.t^2}{2} \to \bf{y_f= 30 +15.t - 4,9t^2}\], la ecuación de velocidad será: \[ V_f = V_o - g.t \to \bf{V_f=15 - 9,8.t}\]
Ahora podemos plantear los distintos apartados que nos piden:
a) ¿Qué altura máxima alcanza el martillo? Está relacionada con la ecuación de posición: \(y_f = 30 + 15.t - 4,9t^2\), pero tiene dos incógnitas, la posición final, es decir su altura máxima, y el tiempo en llegar a dicha altura. Para calcular ese tiempo utilizamos la ecuación de velocidad, \(V_f= 15 -9,8.t\), aplicando la condición de que en la altura máxima la Vf será cero: \[ 0=15-9,8.t \to \bf{t=\frac{15}{9,8} = 1,5 s} \], conocido el tiempo podemos calcular la altura máxima: \[y_{max}= 30 + 15.1,5 -4,9.1,5^2 \to \bf {y_{max}= 41,5 m.}\] Siempre respecto el suelo.
b) El tiempo en llegar al punto más alto se ha calculado antes, los 1,5 segundos.
c) ¿Cuánto tiempo pasó desde el lanzamiento hasta que se encuentra a la mitad de altura del andamio? Si estamos a 30 m la mitad será 15 m. Por tanto, ahora la posición final serán los 15 metros del suelo. Aplicamos la ecuación de posición: \[y_f= 30 + 15.t - 4,9t^2 \to 15 = 30 +15.t -4,9.t^2\] Nos queda una ecuación de segundo grado, reorganizando los términos: \[4,9.t^2 - 15.t -15 = 0\] Esta ecuación, al ser de segundo grado, tiene dos soluciones, t=3,9 s y t=-0,8 s. SÓLO SERÁ VÁLIDA LA POSITIVA.
d) Para calcular la velocidad a los 15 metros, sustituimos en la ecuación de velocidad con el tiempo anterior: \[V_f = 15 -9,8.3,9= \bf{- 23,2 \frac{m}{s}}\] El signo menos nos indica el sentido del movimiento, hacia el suelo (origen de espacios).
e) ¿Tiempo en llegar al suelo? Para hacer este cálculo utilizamos la ecuación de posición, de forma que la posición final ahora es cero, porque ha llegado al suelo (nuestro origen). \[y_f = 30 + 15.t - 4,9.t^2 \to 0=30 + 15.t -4,9.t^2 \to 4,9t^2-15t-30=0\] Dos soluciones: t=4,4 s y t=- 1,4. DE NUEVO SÓLO PUEDE SER VÁLIDA LA POSITIVA.
f) ¿Velocidad en el suelo? Para ello aplicamos la ecuación de velocidad, \(V_f= 15 - 9,8.t\) y sustituimos el tiempo por su valor, t=4,4 s: \[V_f=15-9,8.4,4 = \bf{-28,1 \frac{m}{s}}\]. De nuevo el signo menos nos indica el sentido de movimiento, hacia el suelo (origen de espacios).