Movimiento rectilíneo uniformemente acelerado (MRUA).

Ecuaciones del Movimiento rectilíneo uniformemente acelerado (MRUA).

Un movimiento se considera rectilíneo uniformemente acelerado (MRUA),si su trayectoria es una línea recta y su aceleración permanece constante y es distinta de cero. Al ser rectilíneo, es acelerado porque varía ,sólo, el módulo de la velocidad.

De la definición de aceleración media, al ser rectilíneo es unidimensional, por lo que no es necesario trabajar de manera vectorial: \[\boxed{a_m=\frac{\Delta v}{\Delta t}=\frac{v_f -v_0}{t_f-t_0}}\]

Es muy importante fijarse en el sentido del movimiento del cuerpo para poder asociar los signos más adecuados a nuestra ecuación.

En la ecuación anterior consideramos que el tiempo inicial será cero y reorganizando los términos obtenemos la siguiente ecuación, denominada ecuación de la velocidad: \[\boxed{v_f=v_0 + a.t}\]

Por otro lado, para poder obtener la posición de nuestro cuerpo en movimiento utilizamos la que denominamos ecuación de la posición: \[\boxed{s_f=s_0 + v_0.t + \frac{a.t^2}{2}}\]

s_f → indica la posición final; s₀ → indica la posición inicial; v₀→ es la velocidad inicial; t→ tiempo; a→ aceleración. La diferencia entre s_f y s_0,s_f-s₀_,(Δs),es el desplazamiento. Todos estos parámetros deben ir en las unidades adecuadas y con sus signos correspondientes en función del movimiento del cuerpo.

Otra ecuación que se suele utilizar en este movimiento, es la que relaciona, la posición, la velocidad y la aceleración, para obtenerla despejamos el tiempo en la ecuación de velocidad y lo sustituimos en la ecuación de la posición. La ecuación será: \[\boxed{v^2_f-v^2_0=2.a.\Delta s}\]

Aplicamos lo aprendido

Observa la siguiente imagen y resuelve los apartados que se indican:

mrua

Si suponemos que parte del origen y del reposo, y su aceleración es de 10 m/s², calcula en el S.I:

El tiempo que tarda en alcanzar la velocidad mostrada.
La distancia que recorrió en el momento que alcanzó la anterior velocidad.

Identificamos el punto de partida del coche, nos dice que parte del origen: s₀=0 y del reposo: v₀=0. Pasamos al S.I la velocidad alcanzada, 61,1 m/s. Otro dato es su aceleración, a=10 m/s². Identificamos también signos : movimiento hacia la derecha, por tanto, positivo, se aleja del origen. No es necesario trabajar de manera vectorial al ser unidimensional sin cambios en la dirección.

El tiempo se puede calcular a partir de la ecuación de velocidad: \(v_f=v_0 +a.t\). Despejamos el tiempo y sustituimos:\[t=\frac{v_f-v_0}{a} \to t=\frac{61,1-0}{10}=6,11 s\]
La distancia recorrida: al ser rectilíneo sin cambiar el sentido de movimiento, la posición final, s_f, coincidirá con la distancia recorrida. Aplicamos la ecuación de posición del cuerpo y sustituimos los valores conocidos, en las unidades adecuadas: \[s_f=s_0 + v_0.t+\frac{a.t^2}{2} \to s_f=0+0+\frac{10.6,11^2}{2} = 187 m\]

Un reto

Observa la imagen y responde los distintos apartados:

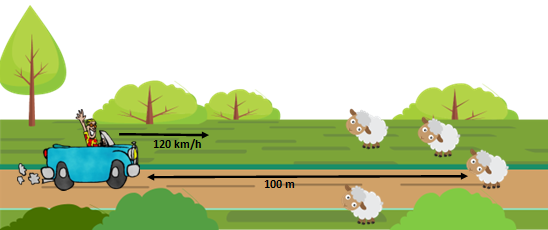¿Qué aceleración debe comunicar el turista al coche para no atropellar a la ovejita que está en el centro de la carretera?
¿Cuánto tiempo tarda en detenerse?
Si no hubiese frenado, ¿cuánto tiempo habría tardado en atropellar a la ovejita?

a) Identificamos el movimiento ,signos, posición de los cuerpos. Consideramos el origen en el punto en el que se encuentra el conductor. Por tanto, la posición inicial, s₀, es cero y la posición final, s_f, los 100 m. El turista debe frenar, la aceleración será negativa, para no atropellar a la ovejita, por tanto, la velocidad final, v_f, debe ser cero.

Planteamos la ecuación de velocidad del turista con su coche: \( v_f= v_0 + a.t\) Tiene dos incógnitas, a y t. Por tanto, debemos utilizar también la ecuación de posición: \( s_f=s_0 + v_0.t + \frac{a.t^2}{2}\).

Sustituimos los datos y planteamos un sistema de dos ecuaciones con dos incógnitas; pero existe otra alternativa, utilizar la otra ecuación del movimiento: \[ v^2_f - v^2_0 = 2 .a.\Delta s\]

v_f=0 ; v₀=120 km/h (33,3 m/s) ; s_f=100 m; s₀=0 ; Recordad que Δs= s_f-s₀ . Sustituimos y calculamos la aceleración pedida:

\(0-33,3^2 = 2. (100-0).a \to a=\frac{-33,3^2}{200} \to a= \bf{- 5,5 \frac{m}{s^2}}\)

b) Para calcular el tiempo sustituimos en la ecuación de velocidad: \(v_f=v_0 + a.t\) y despejamos el tiempo: \[t=\frac{v_f-v_0}{a} \to t=\frac{0-33,3}{-5,5}=\bf{6,1 segundos}\]

c) Si el turista no frena, tendríamos un MRU. Aplicando la ecuación del MRU: \[s_f=s_0 + v.t \to 100=0 + 33,3.t \to t=\frac{100}{33,3}= \bf{3 segundos}\]

Ahora te toca a ti.

Un coche circula por una recta a una velocidad constante de 108 km/h en una vía limitada a 90 km/h. Una moto de la policía, parada en esa zona, arranca y lo persigue con una aceleración de 1,2 m/s². Calcula el tiempo que tarda en alcanzarlo y la distancia recorrida por la policía.

mrua

Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0