Punto de encuentro entre móviles.
Vamos a plantear una situación en la que dos cuerpos en movimiento se encuentran en un punto del recorrido.
Vamos a plantear una situación en la que dos cuerpos en movimiento se encuentran en un punto del recorrido.
Observa el siguiente dibujo de dos ciclistas que salen simultáneamente de dos puntos distintos:


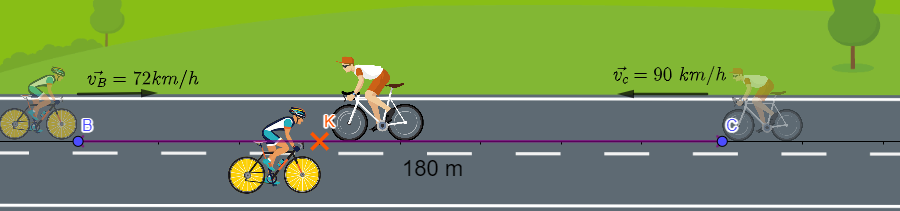
En este cruce, punto K, los dos ciclistas estarán en la misma posición respecto el punto B, por tanto, \[X_B=X_C\], \[20t=180-25t\], despejando el tiempo, t, podremos calcular el tiempo que tardaron en juntarse (cruzarse), \( 45t=180 \to t=4 segundos\)
El punto de encuentro respecto el origen se calcula sustituyendo los 4 segundos en la ecuación de movimiento de B, ciclista que estaba en el origen: \( \bf{X_B=20*4=80 m}\) del punto de origen.
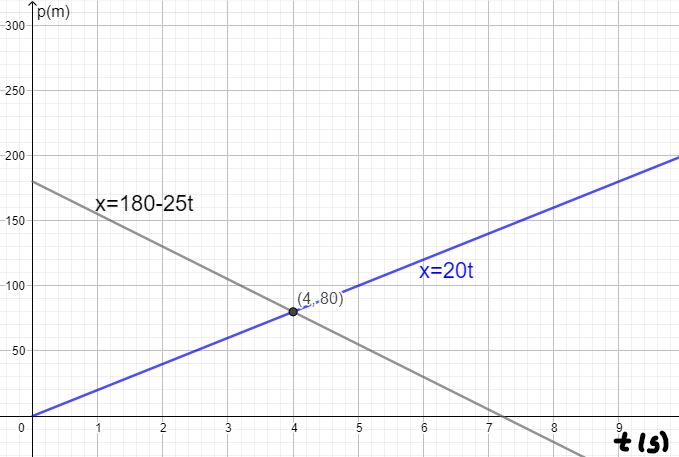
Otra forma de resolverlo sería representar las dos gráficas y el punto en el que se cruzan nos dará el tiempo que tardan y la posición de cruce:
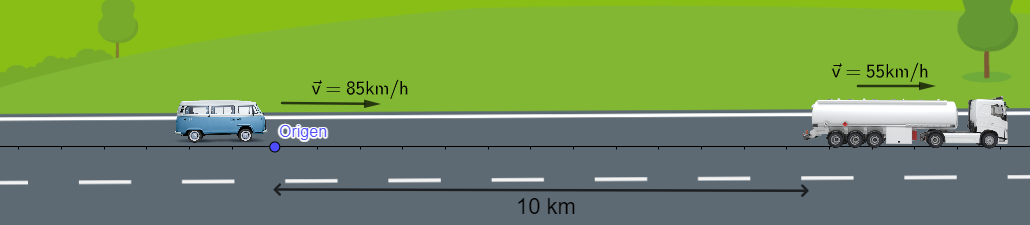
Observa el siguiente dibujo y resuelve los retos que se plantean:
Observa la siguiente imagen de los dos ciclistas saliendo de dos puntos, pero el ciclista C tarda 5 segundos más en salir que nuestro ciclista B.

Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0