Un interval és un subconjunt de la recta real que està format per tots els números compresos entre dos valors anomenats extrems.

• Interval tancat: Correspon a tots els números compresos entre els extrems, tots dos inclosos

\([a, b]=\{x \in \mathbb{R} / a \leq x \leq b\}\)

\(a \leq x \leq b\)

• Interval obert: Correspon a tots els números compresos entre els extrems, exclosos tots dos.

\(] a, b[=\{x \in \mathbb{R} / a<x<b\}\)

\(a<x<b\)

• Interval semiobert o semitancat: Correspon a tots els números compresos entre els extrems, inclòs només un d'ells.

\([a, b[=\{x \in \mathbb{R} / a \leq x < b\}\)	\(]a, b]=\{x \in \mathbb{R} / a <x \leq b\}\)
\(a \leq x<b \)	\(a<x \leq b\)

• Semirecta oberta: Correspon a tots els números majors (o menors) que l'extrem, exclòs el mateix.

\(]-\infty, a[=\{x \in \mathbb{R} / x<a\} \)	\(] a,-\infty[=\{x \in \mathbb{R} / x>a\}\)
\(x<a\)	\(x>a\)

• Semirecta tancada: Correspon a tots els números majors (o menors) que l'extrem, inclòs el mateix.

\(]-\infty, a]=\{x \in \mathbb{R} / x \leq a\} \)	\([a,-\infty[=\{x \in \mathbb{R} / x \geq a\}\)
\(x\leq a\)	\(a\leq x\)

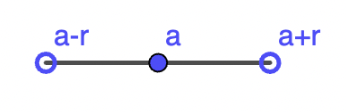
Es diu entorn de centre \(a\) i radi \(r\) a l'interval obert de nombres reals compresos entre \(a-r\) i \(a+r\), és a dir:

\(\left.E_{r}(a)=\{x \in \mathbb{R} / a-r<x<a+r\}=\right] a-r, a+r[\)