Suma y resta de dos números enteros
Observa en el siguiente video el procedimiento para sumar y restar dos números enteros.
¡TE VAS A QUEDAR HELADO!
2. ¿Cómo se opera con números enteros?
Suma y resta de números enteros con paréntesis
Observa en el siguiente video el procedimiento para sumar y restar números enteros cuando llevan paréntesis.
Regla útil:
- Un signo positivo (+) delante de un paréntesis no cambia ningún signo de lo que hay en su interior.
- Un signo negativo (-) delante de un paréntesis cambia el signo de todo lo que hay en su interior.
Sumas y restas combinadas de números enteros
Observa en el siguiente video el procedimiento para realizar sumas y restas combinadas de enteros.
Regla útil: para calcular sumas y restas de enteros, además de operar de izquierda a derecha, también se pueden agrupar los enteros positivos y los enteros negativos.
Ejemplo.
Calcula de dos formas diferentes:
1ª Operando de izquierda a derecha.
(+6) - (+9) - (-7) + (-2) - (-1) = 6 - 9 + 7 - 2 + 1 = -3 + 7 - 2 + 1 = 4 - 2 + 1 = 2 + 1 = 3
2ª Agrupando los enteros positivos y negativos.
(+6) - (+9) - (-7) + (-2) - (-1) = 6 - 9 + 7 - 2 + 1 = (6+7-1) + (-9-2) = 14 - 11 = 3
Sumas y restas combinadas con paréntesis y corchetes
Para resolver sumas y restas combinadas con paréntesis y corchetes, una vez eliminados los paréntesis y los corchetes, podemos operar de 2 formas:
1ª Resolviendo los paréntesis y los corchetes.
Ejemplo.
Calcula resolviendo previamente los paréntesis y corchetes.
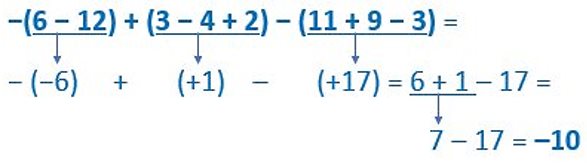
2ª Eliminando los paréntesis y los corchetes.
Ejemplo.
Calcula eliminando previamente los paréntesis y corchetes.
Ejercicios de sumas y restas con enteros
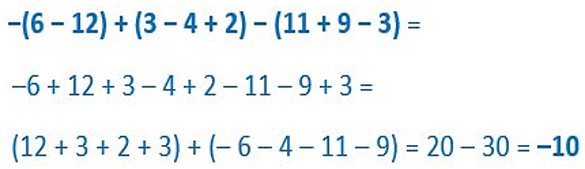
Realiza, en tu cuaderno de clase, las siguientes actividades propuestas.
1) Calcula operando de izquierda a derecha y, a continuación, haz nuevamente el ejercicio, agrupando enteros positivos y negativos:
a) 3 – 7 + 2 – 5 = c) 7 – 10 – 5 + 4 + 6 – 1 =
b) 2 – 6 + 9 – 3 + 4 = d) –6 + 4 – 3 – 2 – 8 + 5 =
2) Elimina los paréntesis y calcula de dos formas diferentes: En primer lugar, operando de izquierda a derecha; a continuación, agrupando enteros positivos y negativos:
a) (–3) – (+4) – (–8) = d) – (–3) – (+2) + (–9) + (+7) =
b) – (–5) + (–6) – (–3) = e) (+8) – (+6) + (–7) – (–4) + (–9) =
c) (+8) – (+6) + (–7) – (–4) = f) – (+4) – (–6) + (+5) + (–8) – (–1) =
3) Calcula resolviendo previamente los paréntesis y corchetes tal y como se hace en el ejemplo resuelto.
Ejemplo → (2 – 9) – [5 + (8 – 12) – 7] = –7 – [5 – 4 – 7] = –7 + 6 = –1
a) 13 – [15 – (6 – 8) + (5 – 9)] = c) (13 – 21) – [12 + (6 – 9 + 2) – 15] =
b) 8 – [(6 – 11) + (2 – 5) – (7 – 10)] = d) [4 + (6 – 9 – 13)] – [5 – (8 + 2 – 18)] =
Multiplicación y división de enteros
Observa en el siguiente video el procedimiento para multiplicar y dividir números enteros.
Observa y aprende las reglas de los signos de la multiplicación y la división de números enteros.
Regla útil. Para hallar el signo del producto o de la división de varios números enteros, se cuenta el número de signos negativos (-). Si es par, el resultado es positivo, y si es impar, negativo.
Ejemplo.
Realiza las siguientes operaciones:
a) –2 · 5 · (–3) · (–1) · (–4) = 120
b) 3 · (–4) · (–1) · (–2) = –24
Ejercicios de multiplicación y división de enteros
Realiza, en tu cuaderno de clase, las siguientes actividades propuestas.
1) Realiza las siguientes multiplicaciones de números enteros teniendo en cuenta las reglas de los signos:
a) (–2) · (–3) · (+4) = c) (+4) · (–3) · (+2) · (+1) =
b) (–1) · (+2) · (–5) = d) (–6) · (–2) · (–5) · (–1) =
2) Realiza las siguientes divisiones de números enteros teniendo en cuenta las reglas de los signos:
a) (–18) : (+3) = d) (–30) : (–10) =
b) (–15) : (–5) = e) (–52) : (+13) : (–2) =
c) (+36) : (–9) = f) (+22) : (+11) : (–1) =
3) Realiza las siguientes operaciones combinadas de multiplicaciones y divisiones. Observa el ejemplo resuelto.
Ejemplo → (–36) : (–3) · (+9) = +72
a) (+125) : (–25) · (+4) = c) (–56) : (–8) · (–2) : (+7) =
b) (–49) : (+7) · (+6) : (–3) = d) (–2) · (+24) : (–12) : (–1) · (+5) =
4) Calcula siguiendo el ejemplo resuelto:
Ejemplo → [(–8) · (+9)] : [(+6) · (–3)] = (–72) : (–18) = +4
a) [(+5) · (–8)] : [(–2) · (–5)] =
b) [(+28) : (–7)] · [(+20) : (–4)] =
c) [(–70) : (+5)] : [(–28) : (+4)] =
Operaciones combinadas con números enteros
Para resolver operaciones combinadas con números enteros debemos seguir el siguiente orden:
Ejemplo 1. Sin paréntesis ni corchetes
Calcula:
15 – 8 · 3 + 18 : 6 – 5 = 15 – 24 + 3 – 5 = (15 + 3) + (–24 –5) = 18 – 29 = –11
Ejemplo 2. Con paréntesis y corchetes
Calcula:
18 – 5 · (8 – 3) – [3 – 16 : (5 + 3)] = 18 – 5 · 5 – [3 – 16 : 8] = 18 – 25 – [3 – 2] = 18 – 25 – 1 = –7 – 1 = –8
Ejercicios de operaciones combinadas con enteros
Realiza, en tu cuaderno de clase, las siguientes actividades propuestas.
1) Realiza las siguientes operaciones combinadas con enteros siguiendo el ejemplo resuelto.
Ejemplo → 15 – 8 · 3 + 18 : 6 – 5 = 15 – 24 + 3 – 5 = (15 + 3) + (–24 –5) = 18 – 29 = –11
a) 18 – 5 · 3 + 7 · 2 – 16 = d) 7 · 3 – 5 · 4 + 18 : 6 =
b) 18 – 15 : 3 + 5 – 30 : 6 = e) 5 · 3 – 4 · 4 + 2 · 6 =
c) 20 : 2 – 11 – 9 · 2 + 5 = f) 25 : 5 – 14 · 2 – 20 : 4 =
2) Calcula resolviendo previamente paréntesis y corchetes como en el ejemplo resuelto.
Ejemplo → 18 – 5 · (3 – 8) = 18 – 5 · (–5) = 18 + 25 = 43
a) 4 · (8 – 11) – 6 · (7 – 9) = e) 28 : (–7) – (–6) · [23 – 5 · (9 – 4)] =
b) (4 – 5) · (–3) – (8 – 2) : (–3) = f) (–2) · (7 – 11) – [12 – (6 – 8)] : (–7) =
c) 15 + 2 · [8 – 3 · 5] = g) [18 + 5 · (6 – 9)] – [3 – 16 : (5 + 3)] =
d) (–3) · (+5) – 3 · [11 + 3 · (5 – 11)] = h) (3 – 6) · [–26 : 13 + 4 · (2 – 3)] : (–3) =
Propiedad Distributiva y Extraer Factor Común
Observa en el siguiente video el procedimiento para aplicar la propiedad distributiva y extraer factor común con números enteros.
Ejercicios de la Propiedad Distributiva y Extraer Factor Común
Realiza, en tu cuaderno de clase, las siguientes actividades propuestas.
1) Calcula, como en el ejemplo resuelto, aplicando la propiedad distributiva:
Ejemplo → (–6) · [5 + (–8)] = (–6) · 5 + (–6) · (–8) = (–30) + (+48) = +18
a) 8 ⋅ [(−5) − (−9) + (+6)] =
b) −10 ⋅ [14 − 13 + 12 − 11] =
2) Calcula, como en el ejemplo resuelto, sacando factor común:
Ejemplo → (–8) · 6 + 3 · 6 + 6 · 10 = 6 · [(–8) + 3 + 10] = 6 · (+5) = +30
a) 25 · 16 – 25 · (–9) =
b) 13 · 6 – 13 · 7 + 13 · 8 – 13 · 9 =
3) Extrae el mayor factor común posible (el m.c.d.) y calcula como en el ejemplo resuelto:
Ejemplo → 250 − 550 + (−20) − (−80) = 250 – 550 – 20 + 80 = 10 · 25 + 10 · (–55) + 10 · (–2) + 10 · 8 = 10 · (25 – 55 – 2 + 8) = 10 · (–24) = –240
a) 42 − (−24) − (+70) − (−112) =
b) 36 – 60 + 144 – (–120) =
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0