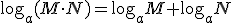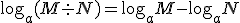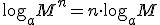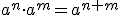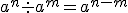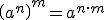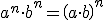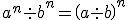Resumen

Importante

Se dice que una ecuación es irracional cuando la incógnita figura dentro de algún radical.

Las ecuaciones logarítmicas son aquellas en las que la incógnita aparece en el argumento o en la base del logaritmo.

Para resolverlas hacemos uso de las siguientes propiedades de los logarítmos:

Recuerda la definición de logaritmo

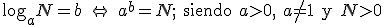$\log_aN = b \ \Leftrightarrow \ a^b=N ; extrm{ siendo }a>0, \ a eq1 extrm{ y }N>0$

y sus principales propiedades

Para resolver las ecuaciones logarítmicas también hay que tener en cuenta:

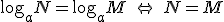$\log_a N=\log_a M \ \Leftrightarrow \ N=M$

Las ecuaciones exponenciales son aquellas en las que la incógnita aparece en el exponente,

Es importante recordar las propiedades de las potencias, porque las vamos a utilizar en la resolución de ecuaciones:

1. $a^n \cdot a^m=a^{n+m}$
2. $a^n \div a^m=a^{n-m}$
3. $$a^n$^m =a^{n \cdot m}$
4. $a^n \cdot b^n=$a \cdot b $^n$
5. $a^n \div b^n=$a \div b $^n$