2.1. Ecuaciones logarítmicas
Las ecuaciones logarítmicas tienen múltiples aplicaciones en todos los campos de la ciencia y la técnica. Habitualmente surgen cuando hay que despejar el exponente de una expresión algebraica.
.jpg) |
| Imagen en Wikimedia Commons. Dominio Público |
Importante
Las ecuaciones logarítmicas son aquellas en las que la incógnita aparece en el argumento o en la base del logaritmo.
Para resolverlas habrá que aplicar la definición y las propiedades de los logarítmos y pasarla a una expresión algebraica.
Cuando resolvemos esta ecuación hay que comprobar si las soluciones obtenidas sirven en la ecuación logarítmica ya que la base de un logaritmo puede ser cualquier número positivo menos el 1 y el argumeto tiene que ser un número positivo.
Veamos algunos ejemplos:
Ejemplo 1
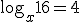
Para resolver esta ecuación tan sólo hay que aplicar la definición de logaritmo y nos queda: 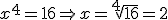 .
.
Podríamos pensar que -2 también es solución de la ecuación algebraica pero hay que recordar que la base de un logaritmo no puede ser un número negativo.
Ejemplo 2
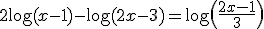
Primero aplicamos las propiedades de los logaritmos hasta quedarnos a ambos lados de la igualdad con un sólo logaritmo:
![\log\[(x-1)^2\]-\log(2x-3) = \log\(\frac{2x-1}{3}\) \ \Rightarrow \ \log \[\frac{(x-1)^2}{2x-3}\]=\log \(\frac{2x-1}{3}\)](eXe_LaTeX_math_14.gif)
De esta forma, los argumentos son iguales por lo que queda la ecuación:
Las soluciones de esta ecuación son x=0 y x=2. x=0 no puede ser solución de la ecuación logarítmica porque cuando sustituimos en la expresión log(x-1) el argumento saldría negativo, x=2 no da problemas en ninguno de los tres logarítmos, por tanto la solución de la ecuación es x=2.Ejemplo 3
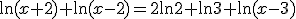
Primero hay que indicar que la base del logaritmo no influye en la resolución de la ecuación, por tanto comenzamos aplicando las propiedades de los logaritmos para agruparlos a ambos lados de la igualdad:
![\ln \[(x+2) \cdot (x-2) \]=\ln (2^2)+\ln (3 \cdot (x-3)) \ \Rightarrow \\ \Rightarrow \ \ln(x^2-4)=\ln \[4\cdot (3x-9) \] \ \Rightarrow \\ \Rightarrow \ \ln(x^2-4)=\ln(12x-36)](eXe_LaTeX_math_13.1.gif)
Igualamos los argumentos y resolvelmos la ecuación resultante: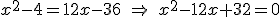
Las soluciones de esta ecuación son x1=4 y x2=8. Ambas soluciones son válidas para la ecuación logarítmica de partida.
En este vídeo puedes ver otro ejemplo:
Vídeo de lasmatematicas.es alojado en Youtube
Comprueba lo aprendido
Ejercicio Resuelto
Resuelve:
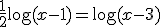
Ejercicio Resuelto
Calcule todas las soluciones de la ecuación ![]() donde
donde ![]() representa el logaritmo en base 10 de x
representa el logaritmo en base 10 de x