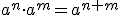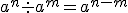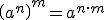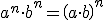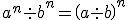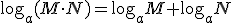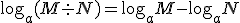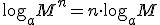2. Ecuaciones exponenciales y logarítmicas

Para la resolución de las ecuaciones tanto exponenciales como logarítmicas es básico recordar las propiedades de las potencias y de los logaritmos.

Importante

Las principales propiedades de las potencias son:

$a^n \cdot a^m=a^{n+m}$

$a^n \div a^m=a^{n-m}$

$$a^n$^m =a^{n \cdot m}$

$a^n \cdot b^n=$a \cdot b $^n$

$a^n \div b^n=$a \div b $^n$

Recuerda la definición de logaritmo

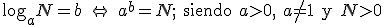$\log_aN = b \ \Leftrightarrow \ a^b=N ; extrm{ siendo }a>0, \ a eq1 extrm{ y }N>0$

y sus principales propiedades

$\log_a (M \cdot N) =\log_a M + \log_a N$

$\log_a (M \div N) =\log_a M - \log_a N$

$\log_a M^n =n \cdot \log_a M$

Para resolver las ecuaciones logarítmicas también hay que tener en cuenta:

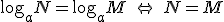$\log_a N=\log_a M \ \Leftrightarrow \ N=M$