2.2. Ecuaciones exponenciales
Las ecuaciones exponenciales suelen surgir en áreas de la ciencia relacionadas con la ecología y medio ambiente. Las mismas nos ayudan a entender mejor el mundo en el que nos movemos.
 |
 |
| Imagen en Wikimedia Commons. Dominio Público | Imagen en Wikimedia Commons. Dominio Público |
Importante
Las ecuaciones exponenciales son aquellas en las que la incógnita aparece en el exponente.
Para resolverlas se aplican las propiedades de las potencias o un cambio de variable hasta llegar a una ecuación de la forma ax=b. Esta se resolverá bien directamente (si b se puede poner como una potencia de base a, igualando los exponentes), bien tomando logaritmos.
Veamos distintos tipos de ecuaciones exponenciales y ejemplos de como resolverlas:
- El tipo más sencillo es de la forma ax=b donde a y b se pueden poner como potencias con la misma base, por ejemplo:
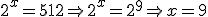 |
- No tan evidente resulta cuando en la ecuación ax=b a y b no se pueden poner como potencias de la misma base. En este caso aplicamos la definición de logaritmo como mostramos en el ejemplo siguiente:
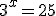 Aplicando la definición de logaritmo quedaría que
Aplicando la definición de logaritmo quedaría que 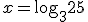
- Si la expresión exponencial va acompañada de un factor de la forma: c·ax=b despejamos ax=b/c y resolvemos la ecuación resultante como alguno de los casos anteriores. Por ejemplo:
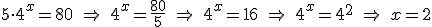 |
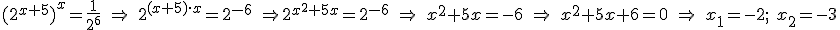 |
Ejercicio Resuelto
Resuelve las siguientes ecuaciones:
a) 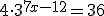 |
b) 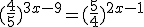 |
c) 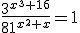 |
Veamos algunos ejemplos:
Ejemplo 1
Cuando en la ecuación aparecen varios términos exponenciales sumando o restando tenemos que recurrir al cambio de variable. Para ver más claro este tipo de ecuación resolvamos algunos ejemplos:
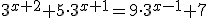
Primero trabajamos con las propiedades de las potencias para que la única expresión exponencial que aparezca sea 3x :
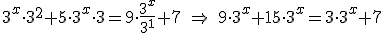
Para que resulte más sencillo trabajar con la anterior expresión hacemos el cambio de variable t=3x, de manera que la expresión quedaría:
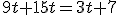
Que no es más que una ecuación polinómica de primer grado muy sencilla de resolver:
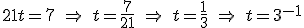
Una vez resuelta, se deshace el cambio de variable y calculamos el valor de x:
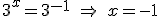
Ejemplo 2
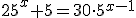
Trabajamos igual que con la ecuación anterior, aunque en este caso hay que tener en cuenta que las exponenciales no tienen la misma base. Lo que hacemos es sustituir 25 por 52 y dejar todo en función de 5x :
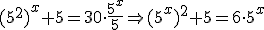
Hacemos el cambio de variable t=5x y resolvemos la ecuación de segundo grado resultante:
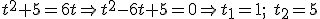
Deshaciendo el cambio quedaría:
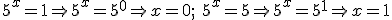
Comprueba lo aprendido
Solución
Solución
También podemos aplicar las propiedades de los logaritmos, vistas anteriormente, para resolver algunas ecuaciones exponenciales.
Ejercicio Resuelto
Resuelve la ecuación ![]()
Parece lógico usar el logaritmo de la misma base que la de la potencia para poder despejar la incógnita.
Ejercicio Resuelto
Resuelve la ecuación ![]()