Nº decimal

Un número decimal se compone de dos partes separadas por una coma:

• La parte a la izquierda de la coma se llama parte entera.
• La parte a la derecha de la coma se llama parte decimal.

Parte decimal

Cada una de las cifras de la parte decimal recibe su propio nombre:

• Si una unidad la dividimos en diez partes obtenemos una DÉCIMA (diez décimas forman una unidad).
• Si una unidad la dividimos en cien partes obtenemos una CENTÉSIMA (cien centésimas forman una unidad).
• Si una unidad la dividimos en mil partes obtenemos una MILÉSIMA (mil milésimas forman una unidad). 

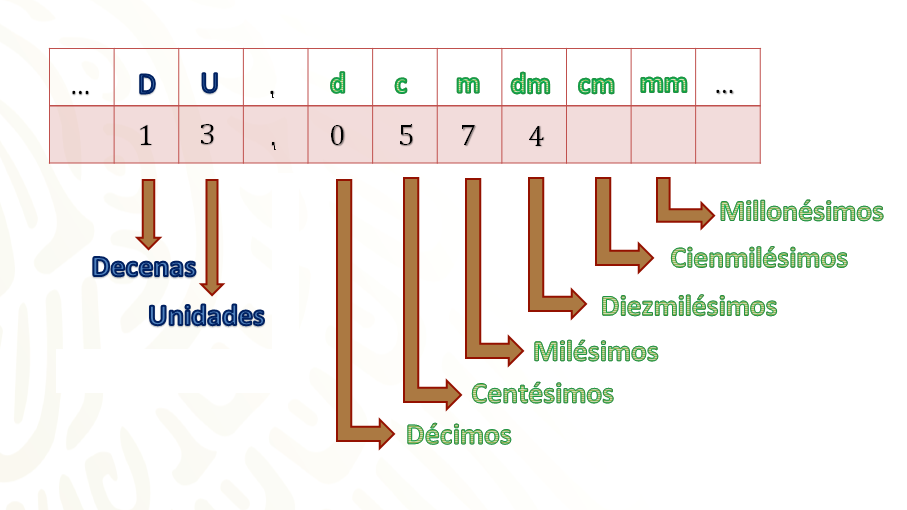
Una unidad se divide en 10 décimas que a su vez se divide en 10 centésimas que a su vez se divide en 10 milésimas y así sucesivamente.

Por lo tanto tendremos:

1 U = 10 d 1 U = 100 c 1 U = 1.000 m 1 U = 10.000 dm 1 U = 100.000 cm 1 U = 1.000.000 ml

1 d = 0'1 U = 1/10 U  1 c = 0'01 U = 1/100 U 1 m = 0'001 U = 1/1.000 U 1 dm = 0'0001 U = 1/10.000 U 1 cm = 0'00001 U = 1/100.000 U 1 ml = 0'000001 U = 1/1.000.000 U

La milésima

Ceros 

Si añadimos ceros a la derecha de un número decimal no aportan información y pueden ser eliminados.

Por lo tanto:

• Una lata de refresco de 0'33 litros y una de 0'330 litros tendrán la misma capacidad.
• Una bandeja de 0'5 kilogramos de manzanas y otra de 0'500 kilogramos de naranjas tendrán la misma masa.
• Una caja de galletas por la hay que pagar 2€ y otra cuyo precio es de 2'00€ costarán lo mismo.

Orden

Para ordenar dos números decimales:

1. Comparamos las partes enteras: Será mayor el de mayor parte entera.
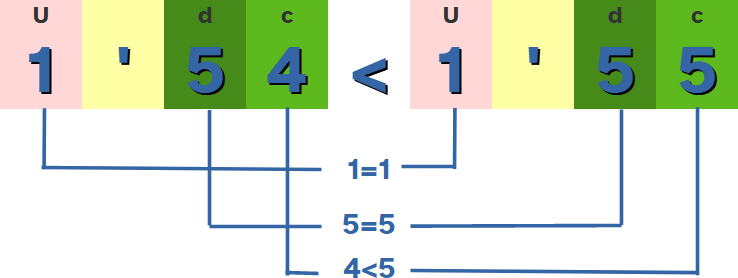
2. Comparamos las décimas: Si las partes enteras son iguales será mayor el que tenga mayor la cifra correspondiente a las décimas.
3. Comparamos las centésimas: Si las partes enteras y las décimas son iguales será mayor el que tenga mayor la cifra correspondiente a las centésimas.
4. Comparamos las milésimas: Si las partes enteras, las décimas y las centésimas son iguales será mayor el que tenga mayor la cifra correspondiente a las milésimas.
5. Continuamos comparando de izquierda a derecha.

A continuación tienes un juego que te permite repasar el orden de números decimales.

J2RE

Representación

Los números decimales se representan en la recta numérica.

Una vez que tenemos representados en la recta numérica los números naturales:

\pmb{\mathbb N}

...y los números enteros:

\pmb{\mathbb Z}

... es el momento de representar un número decimal.

Para ello, tenemos que ubicarlo entre los dos números enteros donde está comprendido.

Se divide el segmento que une estos dos números enteros (menor y mayor entero que el número decimal) en 10 partes iguales para las décimas, 100 partes iguales para las centésimas,...y así sucesivamente, hasta llegar al número decimal.

En la práctica, procederíamos como sigue:

Para representar, por ejemplo, el número decimal 1'9 tomaríamos el segmento de la recta numérica comprendido entre 1 y 2.

Lo dividimos en 10 partes (colocamos 9 "rayitas") ya que el número decimal llega hasta las décimas y nos quedamos con la novena.

Así quedaría representado el número 1'9.

Si quisiéramos representar el número 2'57 nos situaríamos entre los dos números enteros donde se encuentra este número, en este caso entre 2 y 3.

Luego seguiríamos con las décimas y nos situaríamos entre 2'5 y 2'6 ya que el número decimal se encuentra entre estos dos y llega hasta las centésimas. 

Dividiríamos este segmento en 10 partes y nos quedaríamos con la séptima.

A continuación tienes la siguiente actividad para practicar la representación de los números decimales.