Ecuaciones del m.a.s.
Conocimiento previo
DERIVADAS TRIGONOMÉTRICAS (Matemáticas 1º Bachillerato)
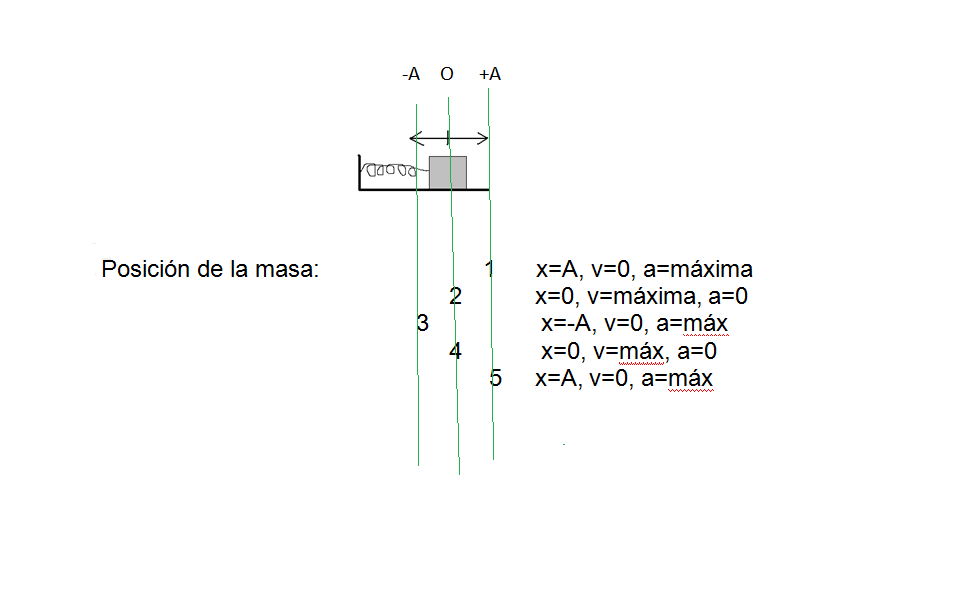
Magnitudes del m.a.s.: x, v, a => OSCILADOR ARMÓNICO
x = ecuación de la elongación (posición)
v = velocidad (rapidez) de vibración
a = aceleración
Fuente: Vicente Gómez Toraya (autor de la REA)
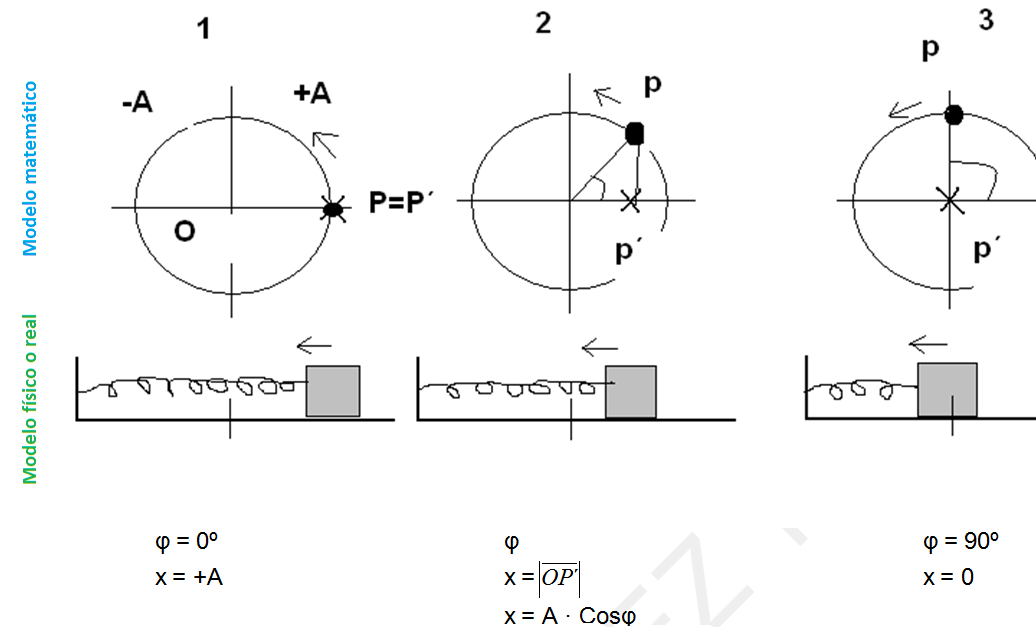
Ecuación del m.a.s. relacionada con el movimiento circular uniforme (comparación del modelo físico o real con el matemático):
P = ángulo girado representado en la circunferencia = ●
P´= móvil moviéndose de máx-mín. = x
P´ es la proyección de P sobre el diámetro
φ = FASE = ángulo girado
Fuente: Vicente Gómez Toraya (autor de la REA)
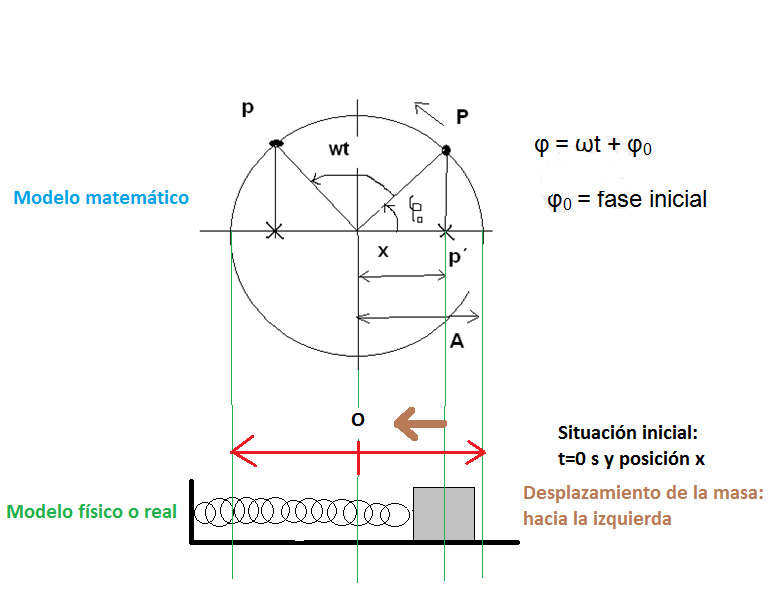
En general, debemos considerar una fase inicial φ0 desde donde comienza el m.a.s.:
Casos particulares => x = +A, φ0 = 0º => un extremo
=> x = 0, φ0 = 90º => origen
Fuente: Vicente Gómez Toraya (autor de la REA)
Entonces, las ecuaciones del movimiento:
Elongación (posición) => x = A · Cos (ωt + φ0)
Rapidez (velocidad) => v = dx/dt = - A · ω · Sen(ωt + φ0)
Aceleración => a = dv/dt = - A · ω2 · Cos(ωt + φ0) = - ω2 · x
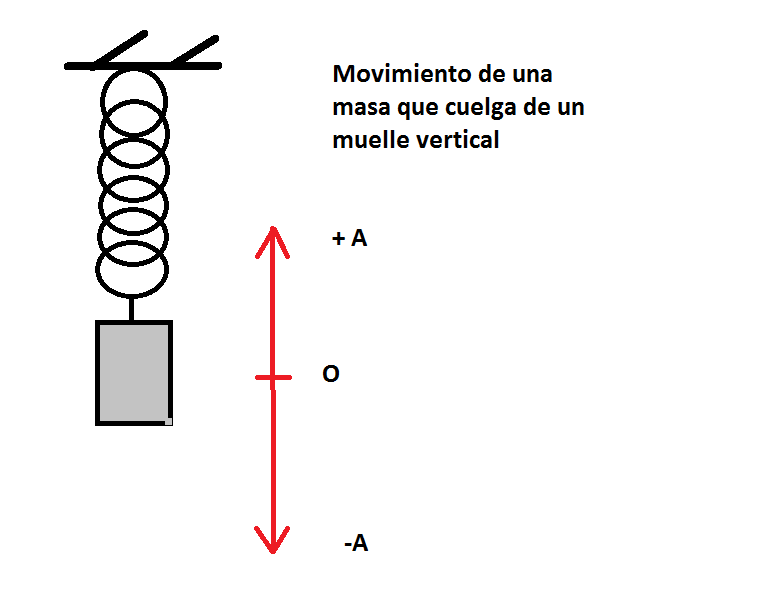
Disponemos de un muelle que cuelga de un techo,
Fuente: Vicente Gómez Toraya (autor de la REA)
Obtener las ecuaciones del movimiento: posición, velocidad y aceleración.